Diffusion Model学习笔记其一

概念理解

Diffusion

模型就是进行一步一步的加噪、去噪的过程

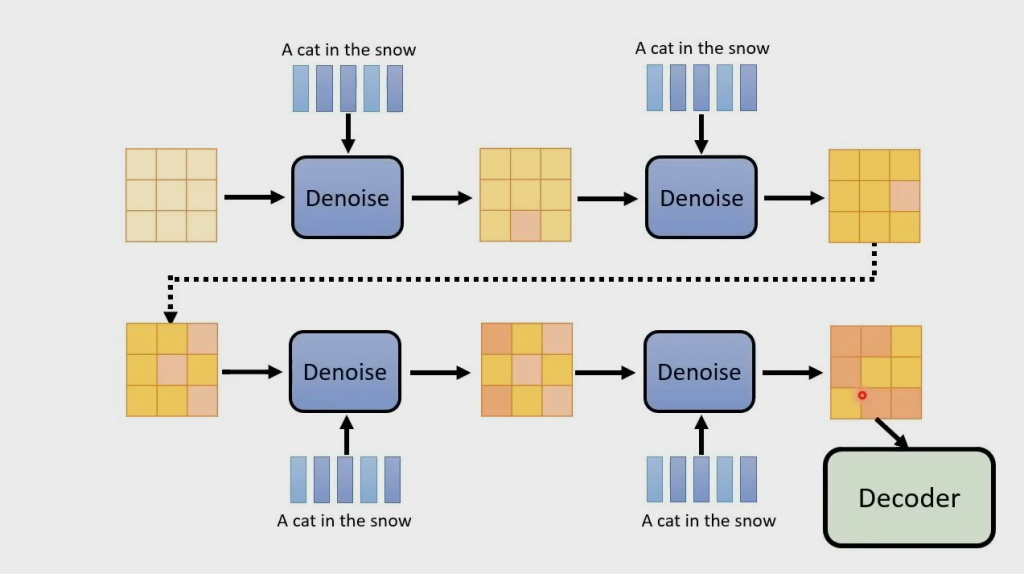
Denoise Process（Reverse Process）

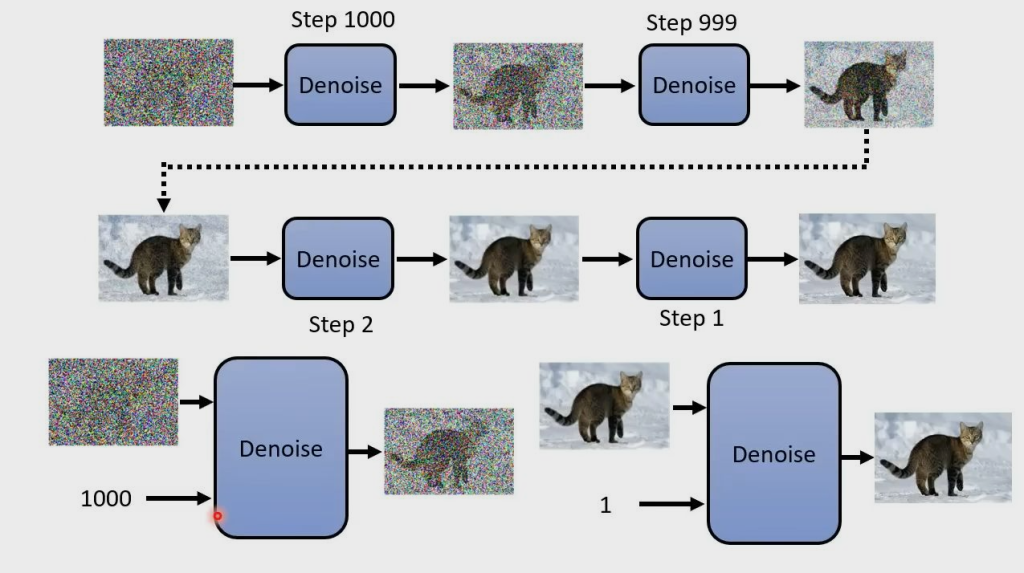
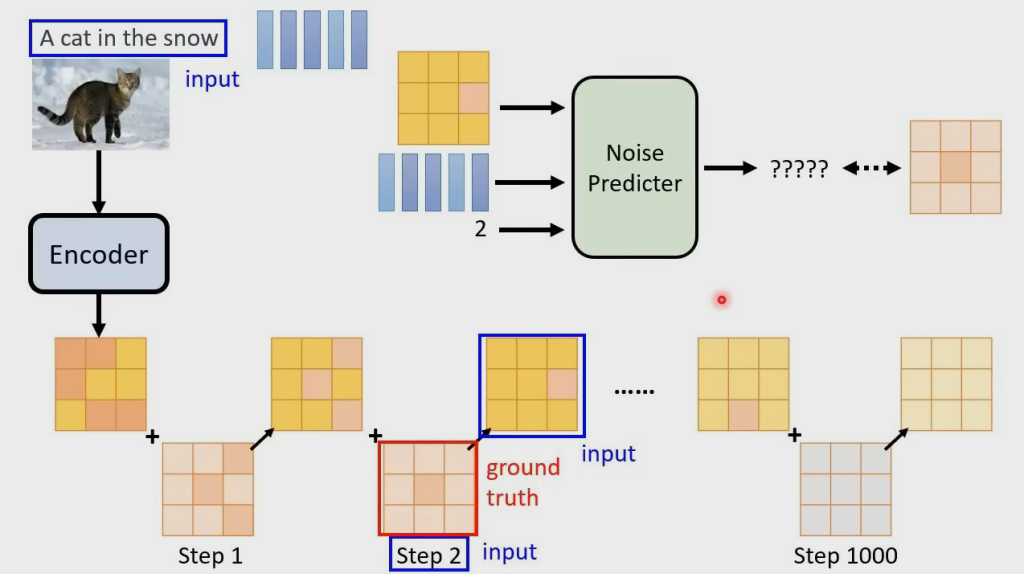
由于每次的 Denoise 都进行相同操作，因此要 Step 进行区别，Step 表示 noise 的严重程度

每个 Denoise Model 里有一个 Noise Predicter，用来预测并生成输入图片的噪声，再将输入图片减去预测的噪声，得到降噪后的输出图片

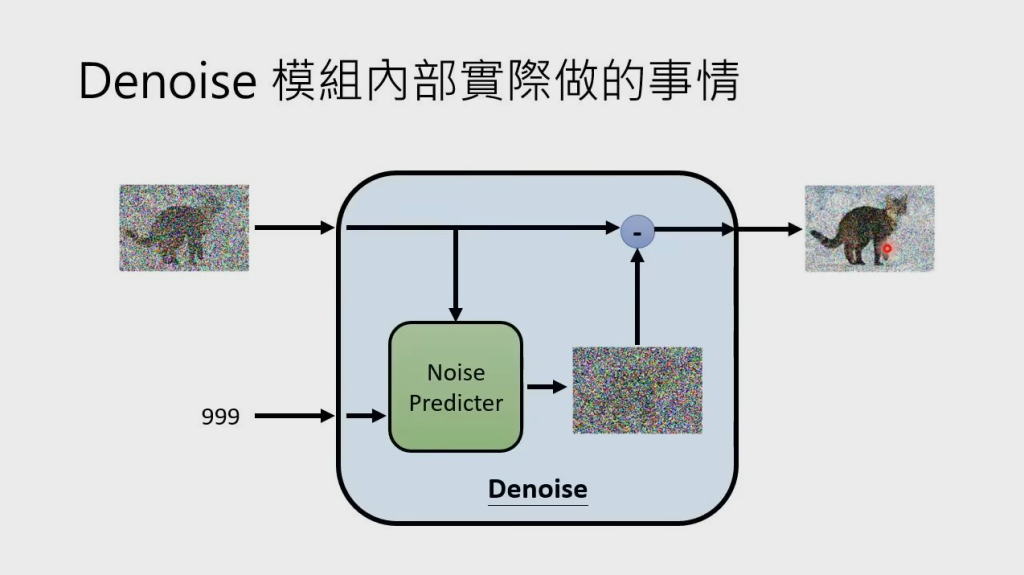
Noise Predicter 如何预测噪声？需要训练，因此需要知道图片的真实噪声 Ground truth

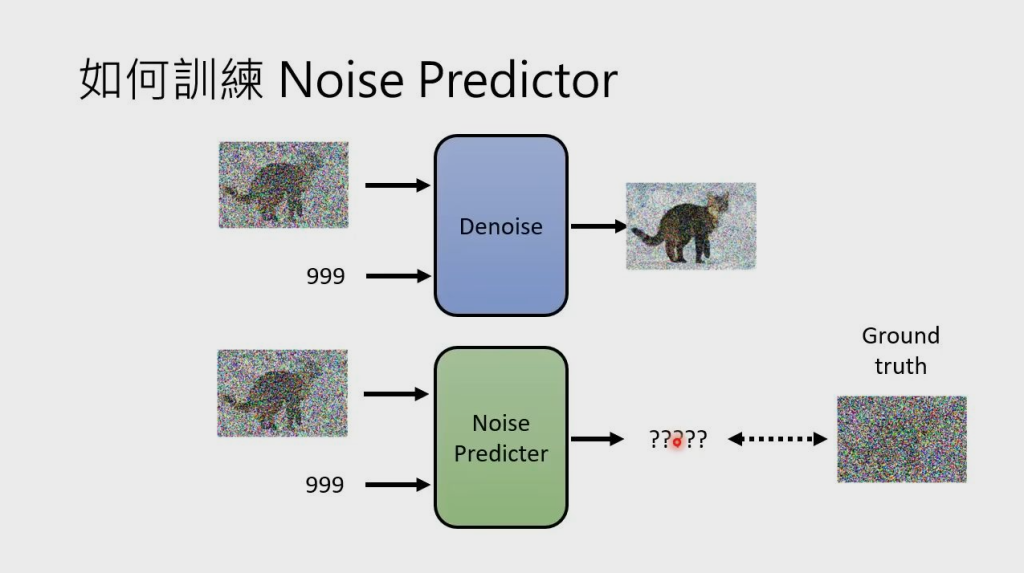
如何得到 Ground truth？只需要向真实图片中人为加入噪声，这个过程也就是模型的加噪过程（Forward Process）

Diffusion Process（Forward Process）

我们记：

• $T$ ：总步数

• $x_0,x_1,\cdots,x_T$ ：每一步产生的图片。其中 $x_0$ 为原始图片，$x_T$ 为纯高斯噪声

• $\epsilon \sim N(0,I)$ ：为每一步添加的高斯噪声

• $q(x_t|x_{t-1})$ ：$x_t$ 在条件 $x = x_{t-1}$ 下的概率分布（$q(x_t|x_{t-1})$ 表示 Difusion Process，$p_\theta(x_{t-1}|x_t)$ 表示 Denoise Process，$\theta$ 表示模型参数）

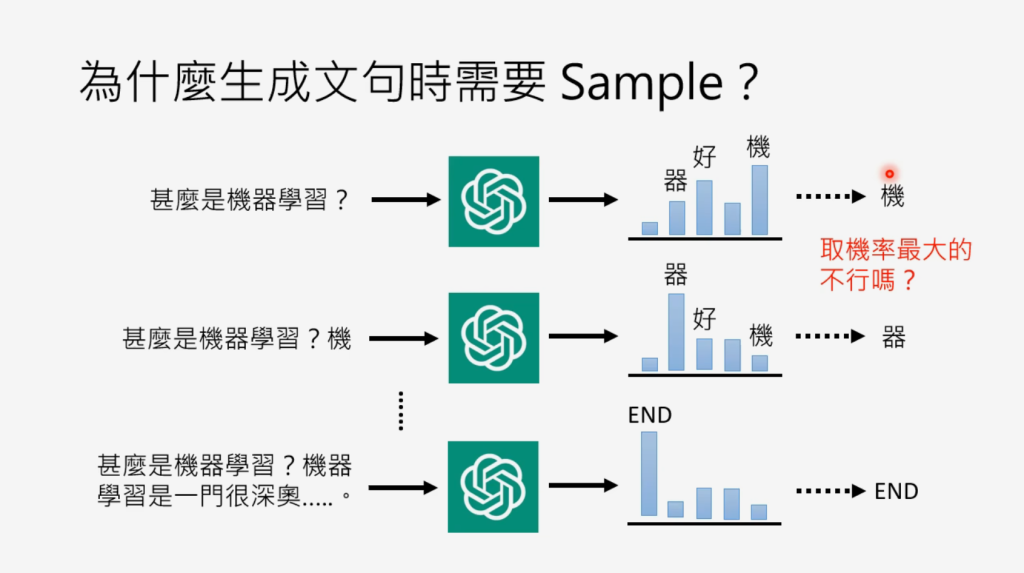
  那么根据以上流程图，我们有： $x_t = x_{t-1} + \epsilon = x_0 + \epsilon_0 + \epsilon_1 + \cdots + \epsilon$ 根据公式，为了知道 $x_t$ ，需要sample好多次噪声，感觉不太方便，能不能更简化一些呢

重参数

我们知道随着步数的增加，图片中原始信息含量越少，噪声越多，我们可以分别给原始图片和噪声一个权重来计算 $x_t$ ：

• $\overline \alpha_1,\overline \alpha_2,\cdots,\overline \alpha_T$ ：一系列常数，类似于超参数，随着 $T$ 的增加越来越小。

则此时 $x_t$ 的计算可以设计成：$x_t=\sqrt{\overline \alpha_t}x_0 + \sqrt{1-\overline \alpha_t}\epsilon$

现在，我们只需要sample一次噪声，就可以直接从 $x_0$ 得到 $x_t$ 了。

接下来，我们再深入一些，其实 $\overline \alpha_1,\overline \alpha_2,\cdots,\overline \alpha_T$ 并不是我们直接设定的超参数，它是根据其它超参数推导而来，这个“其它超参数”指：

• $\beta_1,\beta_2,\cdots,\beta_T$ ：一系列常数，是我们直接设定的超参数，随着T的增加越来越大

则 $\overline \alpha$ 和 $\beta$ 的关系为：

$\alpha_t = 1 - \beta_1 \ ,\ \overline \alpha_t = \alpha_1 \alpha_2 \cdots \alpha_t$

这样从原始加噪到 $\beta \ ,\ \alpha$ 加噪，再到 $\overline \alpha$ 加噪，使得 $q(x_t|x_{t-1})$ 转换成 $q(x_t|x_0)$ 的过程，就被称为重参数(Reparameterization)

文生图

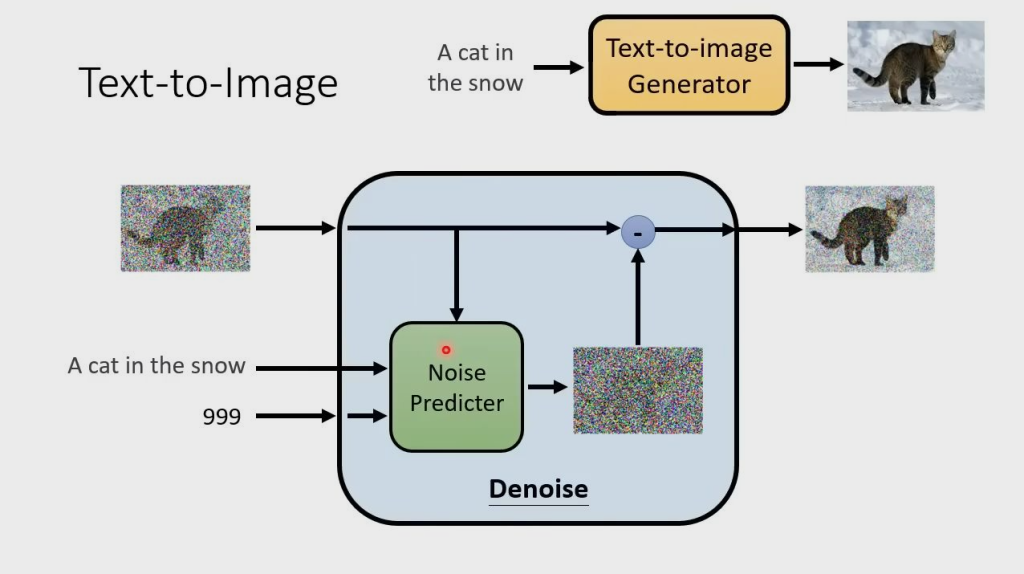
文生图，就是 Denoise 中的 NoisePredicter 多一个额外的输入 word，预测时根据输入图片、Step 和 word 生成 database 中 word 对应图片的噪声。以下为模型的一般公式：

• Text Encoder: 一个能对输入文字做语义解析的Encoder，一般是一个预训练好的模型。在实际应用中，CLIP模型由于在训练过程中采用了图像和文字的对比学习，使得学得的文字特征对图像更加具有鲁棒性，因此它的text encoder常被直接用来做文生图模型的text encoder（比如DALLE2）
• Generation Model： 输入为文字token和图片噪声，输出为一个关于图片的压缩产物（latent space）。这里通常指的就是扩散模型，采用文字作为引导（guidance）的扩散模型原理
• Decoder：用图片的中间产物作为输入，产出最终的图片。Decoder的选择也有很多，同样也能用一个扩散模型作为Decoder

Stable Diffusion

有三个组件：Encoder，Generation Model，Decoder

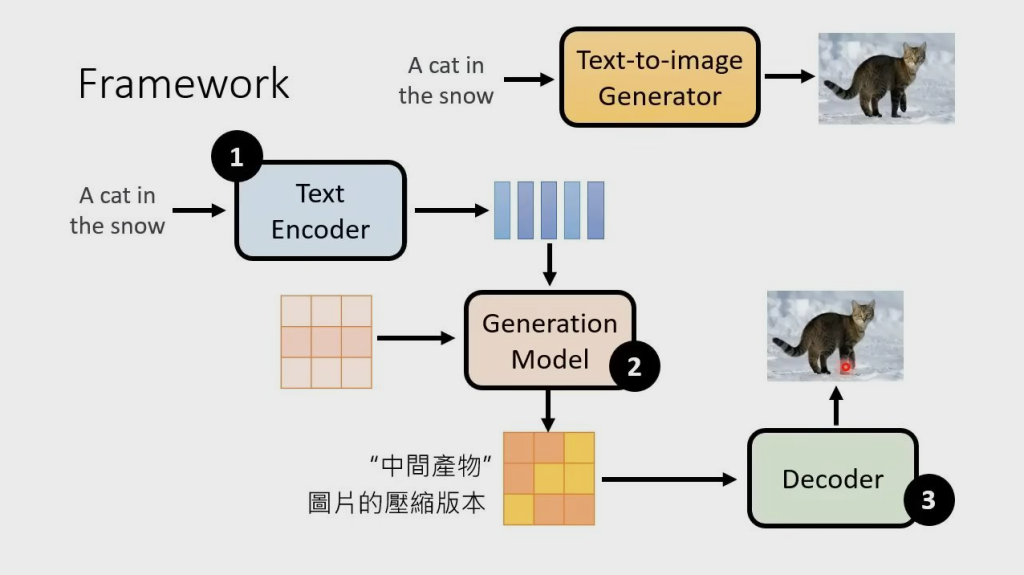
Encoder：把输入内容转换为向量

Generation Model：生成模型，一般为 Diffusion 模型，左边的输入是噪声

Decoder：把压缩版本的图片转换为原本的图片

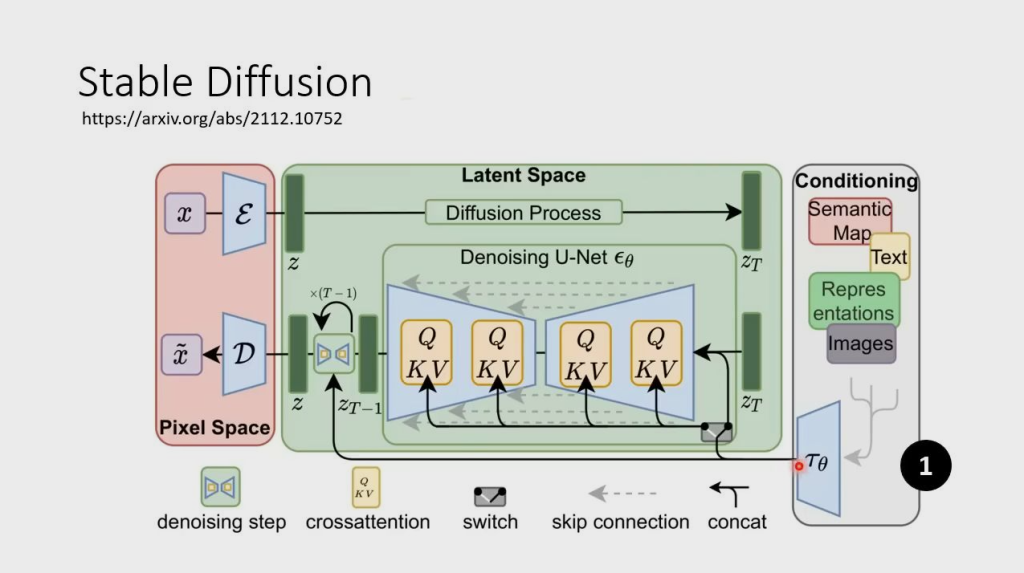
图中从右到左三个框即 Encoder、Generation Model、Decoder

Encoder

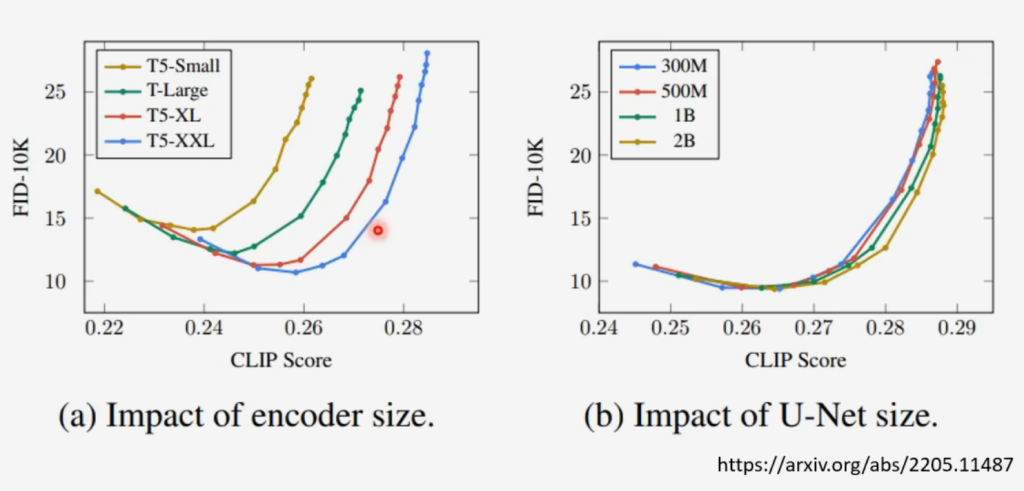
上图说明文字的 Encoder 对生成模型比较关键，而 Diffusion Model 的大小对提升模型的帮助有限

FID——衡量模型生成图片质量的指标

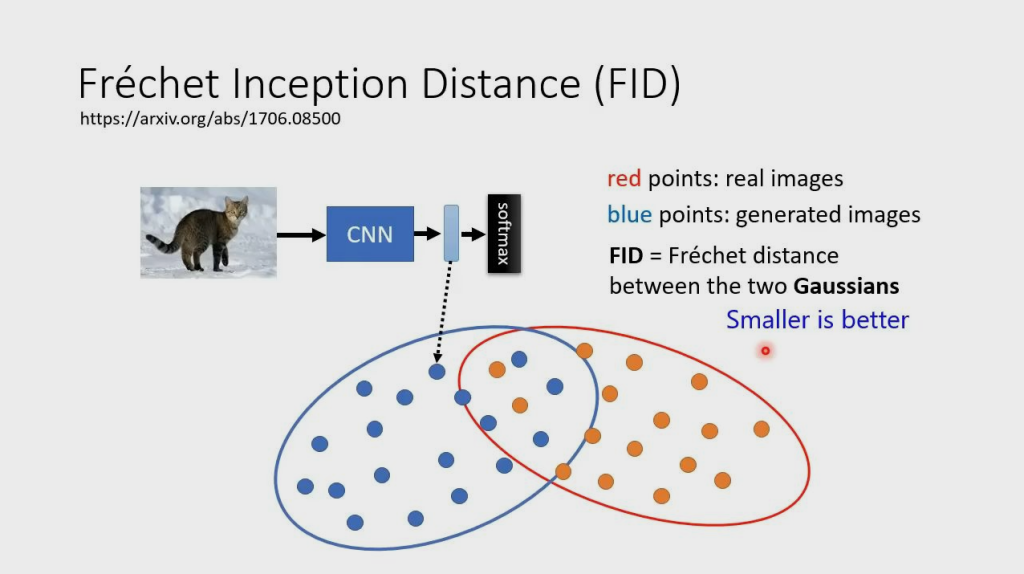
• FID 是生成图像和真实图像在特征空间中的分布距离，距离越小，两图片越像，反之越不像
• FID 假设生成图像和真实图像在特征空间的分布都是高斯分布，然后计算这两个高斯分布的距离

CLIP——对比语言图像预训练

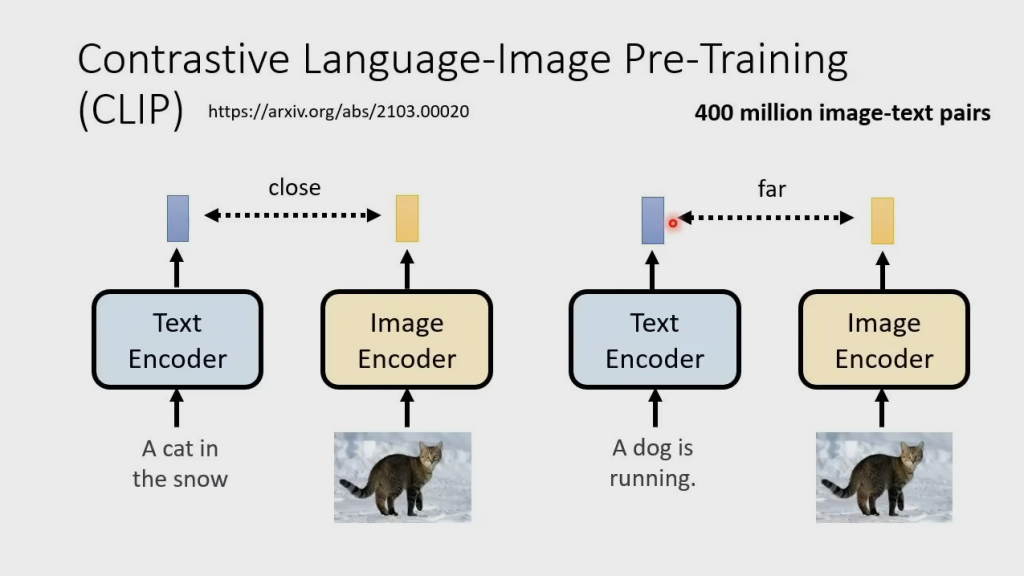
CLIP 有一个 Text Encoder 和一个 Image Encoder，把输入的文字和生成的图片丢进去，转换成两个对应的向量，如果 text 和 image 是成对的，那么这两个向量越近越好；反之越远越好

Decoder

训练 Decoder 时不需要图片与文字相对应的训练数据

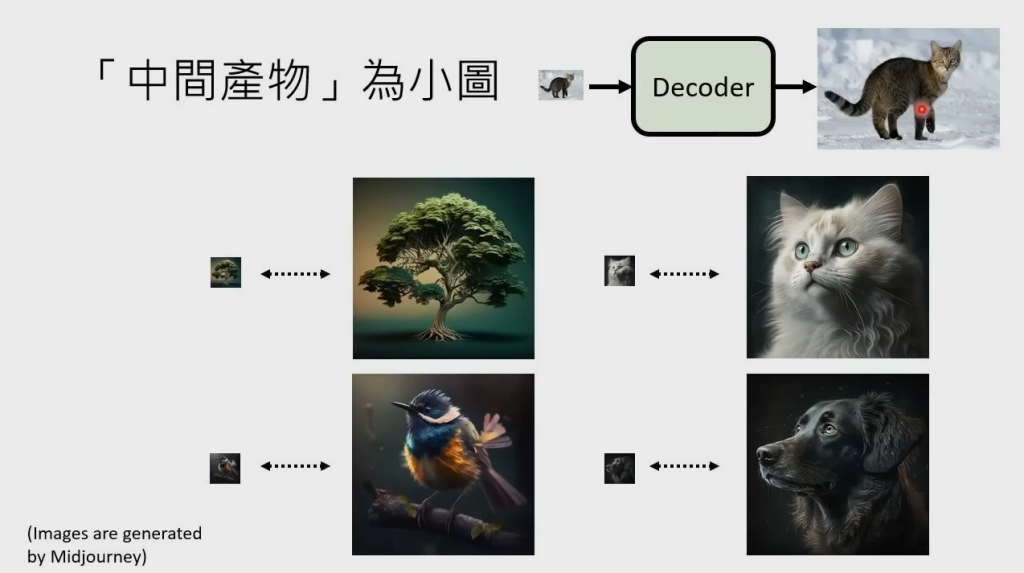
• 当 Decoder 输入是压缩小图时，我们只需要对原始图片进行下采样，变成小图，然后用小图和原始图片组成成对的数据集去训练 Decoder

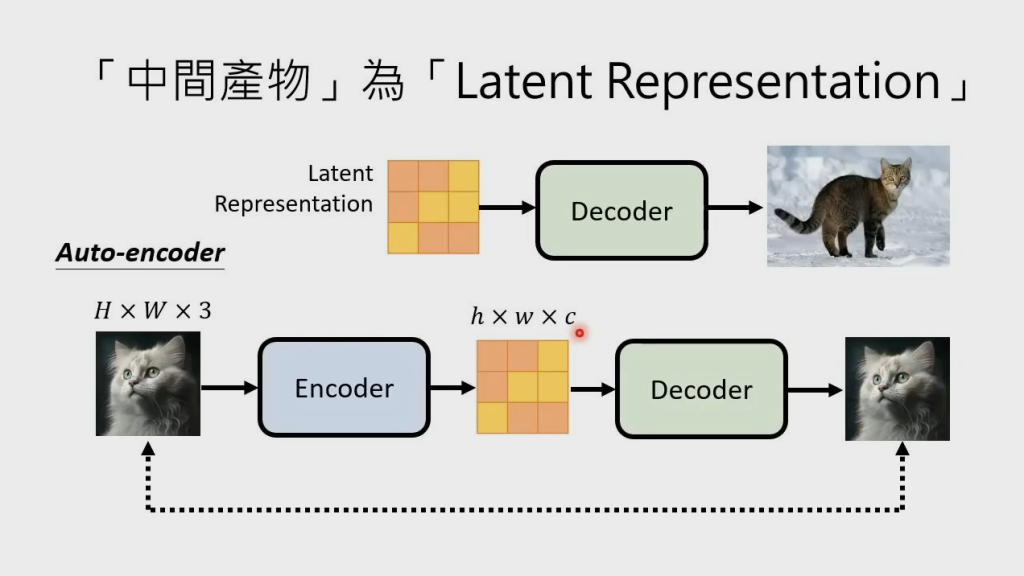
• 当 Decoder 输入是 Latent Representation 时，需要训练一个 Auto-encoder，这个 Auto-encoder 要做的事，就是将原始图片输入到 encoder 中，得到图片的 Latent Representation，然后将其输入到 Decoder 中，得到图片，使得到的图片与输入的图片越相近越好。训练完就可以直接用这个 Auto-encoder 中的 Decoder 了
• Latent Representation 补充：下图中图片上方的 h 表示高，w 表示宽，c 表示每个像素（每个块）用几个数表示

Generation Model

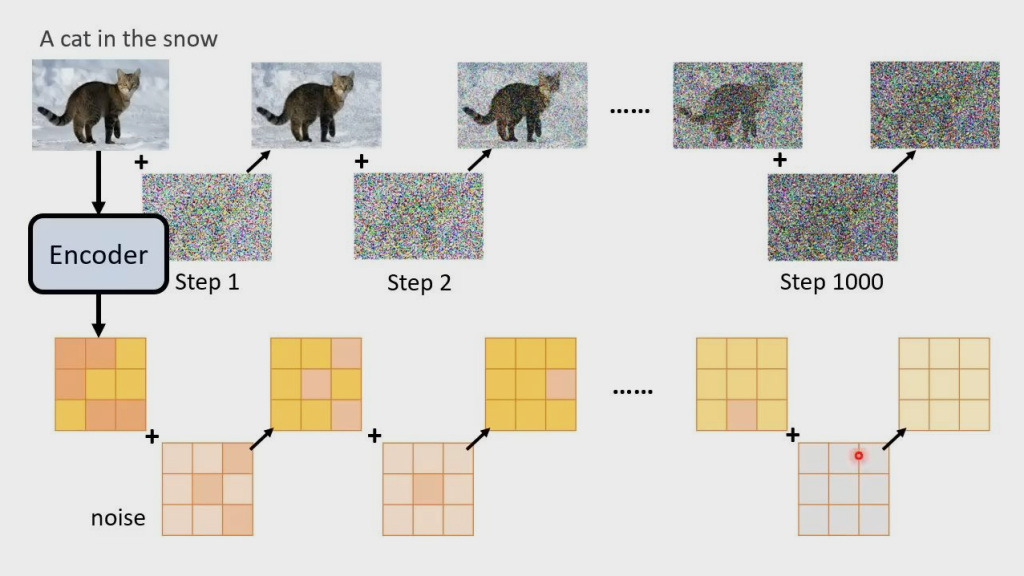
用 Diffusion Model 的话，跟正常 Diffusion Model 的流程基本一样，只是原本 Encoder 时噪声是加在图片上的，现在模型产生的中间产物可能不是图片了，所以改为把噪声加在中间产物上（如 Latent Representation）

下图为改变后的流程

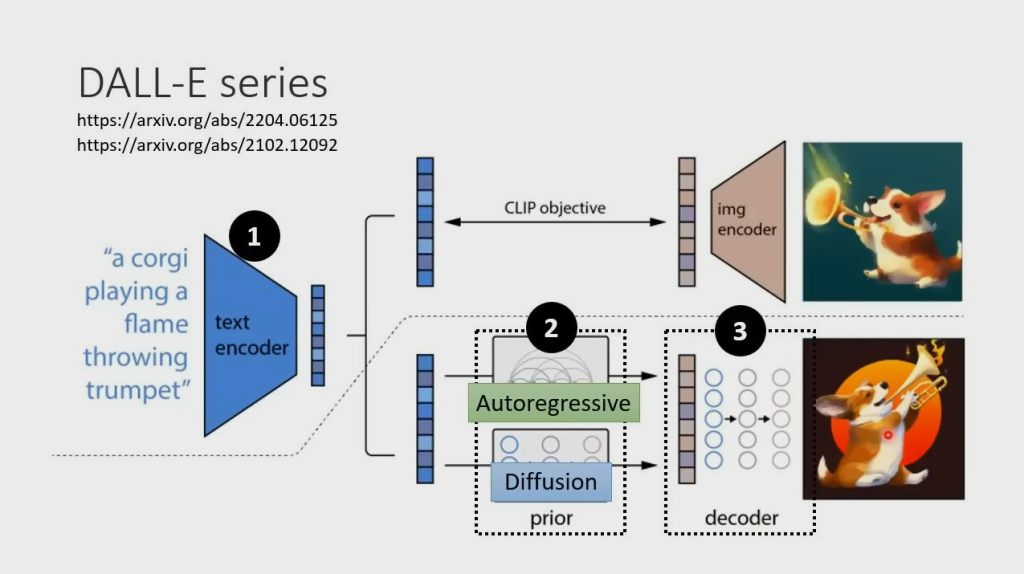
DALL-E series

跟 Stable Diffusion 框架差不多，也是三部分，Encoder、prior 和 Decoder，其中 prior 可以选用 Diffusion，也可以选用 Autoregressive（因为这部分生成的是图片的压缩版本，所以开销不是很大）

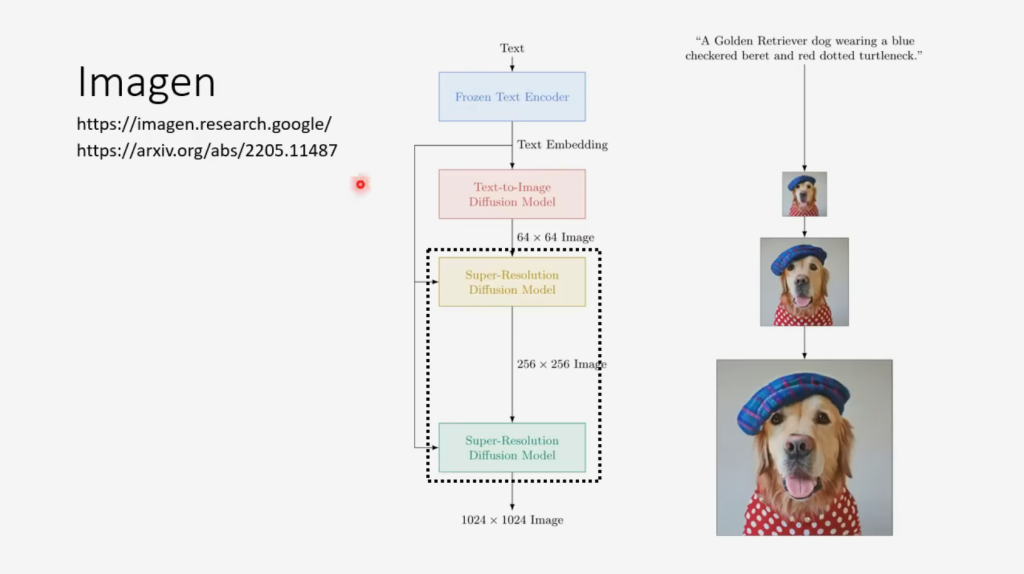
Imagen

谷歌的Imagen，小图生大图，同理

Algorithm

Algorithm1 Training

上图红框中，t 越大，$\overline \alpha _t$ 越小，表示表示原始图片占比越小，噪声占比越大

在重参数的表达下，第t个时刻的输入图片可以表示为：$x_t = \sqrt{\overline \alpha _t}x_0 + \sqrt{1-\overline \alpha _t}\epsilon$

也就是说，第t个时刻sample出的噪声 ，就是我们的噪声真值

而我们预测出来的噪声为：$\epsilon (\sqrt{\overline \alpha _t}x_0 + \sqrt{1-\overline \alpha _t}\epsilon ,t)$ ，其中 $\theta$ 为模型参数，表示预测出的噪声和模型相关

那么易得出我们的loss为：$loss = \epsilon - \epsilon_0(\sqrt{\overline \alpha_t}x_0 + \sqrt{1-\overline \alpha_t}\epsilon ,t)$

我们只需要最小化该loss即可

由于不管对任何输入数据，不管对它的任何一步，模型在每一步做的都是去预测一个来自高斯分布的噪声。因此，整个训练过程可以设置为：

• 从训练数据中，抽样出一条 $x_0$（即 $x_0 \sim q(x_0)$ ）
• 随机抽样出一个timestep（即 $t \sim Uniform(\{1,\cdots,T\})$）
• 随机抽样出一个噪声（即 $\epsilon \sim N(0,I)$）
• 计算： $loss = \epsilon - \epsilon_0(\sqrt{\overline \alpha_t}x_0 + \sqrt{1-\overline \alpha_t}\epsilon ,t)$
• 计算梯度，更新模型，重复上面过程，直至收敛

想象中，噪声是一次一次加上去的，denoise 也是一次一次去的，但实际上，noise 和 denoise 都是通过加权方式一次加上或去掉的

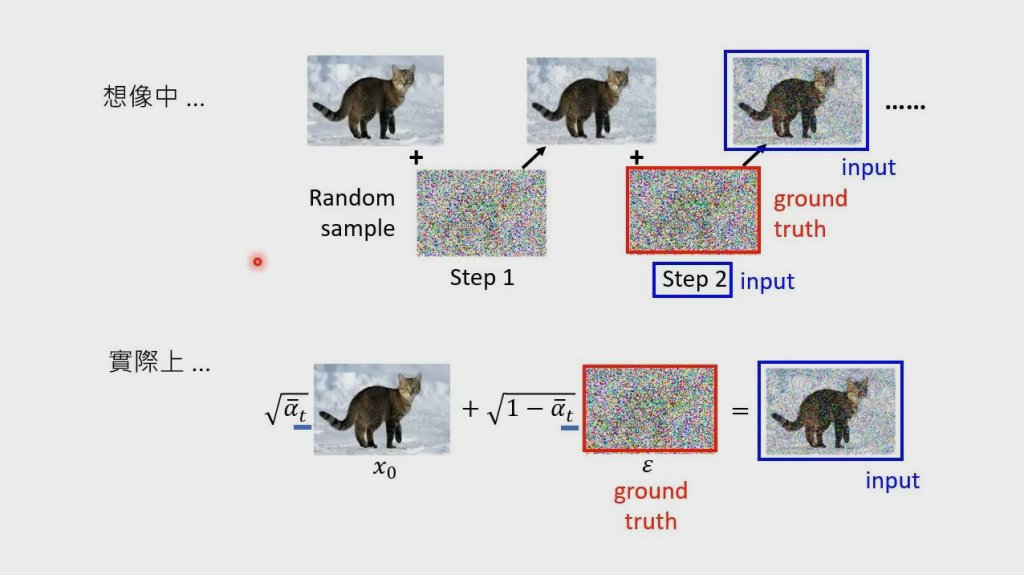
Algorithm2 Sampling

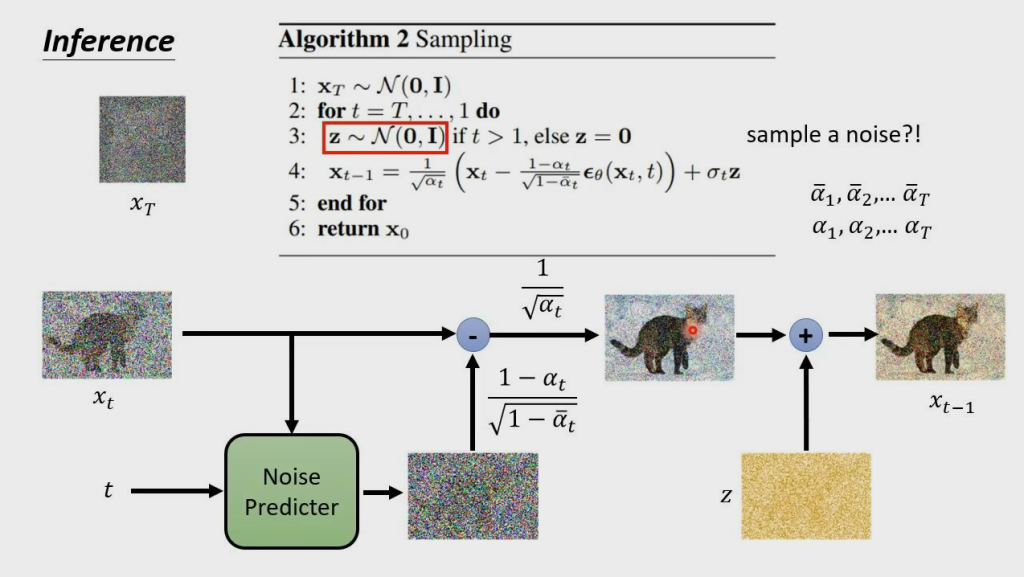
与想象不同的是，denoise 后的图片，又加了一次 noise，才输出结果

对于训练好的模型，我们从最后一个时刻（T）开始，传入一个纯噪声（或者是一张加了噪声的图片），逐步去噪。

根据 $x_t = \sqrt{\overline \alpha_t}x_0 + \sqrt{1-\overline \alpha_t}\epsilon$ ，我们可以进一步推出 $x_t$ 和 $x_{t-1}$ 的关系（上图的前半部分）。而图中 $\sigma_t z$ 一项，则不是直接推导而来的，是我们为了增加推理中的随机性，而额外增添的一项。可以类比于GPT中为了增加回答的多样性，不是选择概率最大的那个token，而是在topN中再引入方法进行随机选择

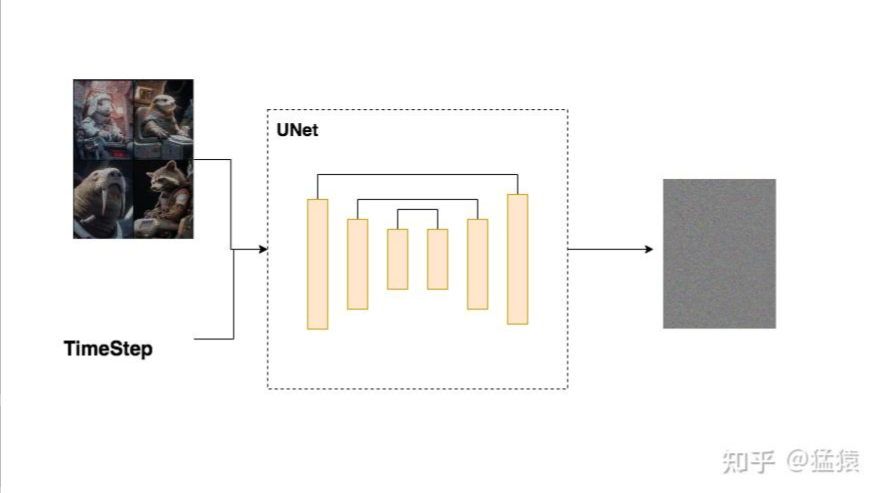
Unet架构

上文中Diffusion Model的Noise Predicter，即Unet模型，分为两个部分：Encoder 和 Decoder 。

在Encoder部分中，Unet模型会逐步压缩图片的大小；在Decoder部分中，则会逐步还原图片的大小。同时在Encoder和Decoder间，还会使用“残差连接”，确保Decoder部分在推理和还原图片信息时，不会丢失掉之前步骤的信息。

整体过程示意图如下，因为压缩再放大的过程形似"U"字，因此被称为Unet：

下面我们通过输入一张32*32*3大小的图片来观察DDPM Unet运作的完整流程

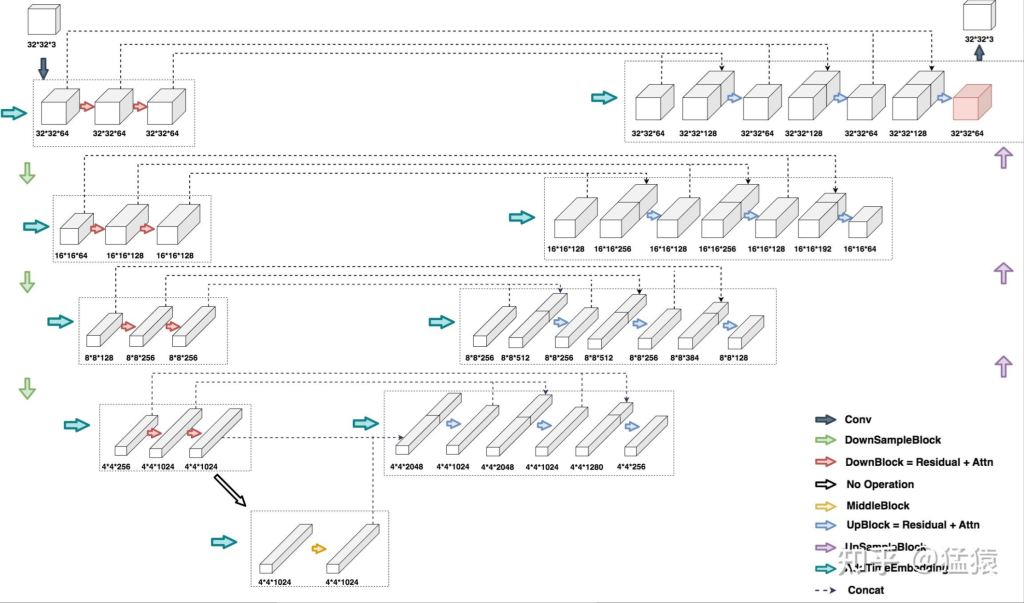
左半边为Encoder部分，右半边为Decoder部分，最下面为MiddleBlock

在Encoder部分的第二行，输入是一个16*16*64的图片，它是由上一行最右侧32*32*64的图片压缩而来(DownSample)。对于这张16*16*64大小的图片，在引入time_embedding后，让它们一起过一层DownBlock，得到大小为16*16*128 的图片。再引入time_embedding，再过一次DownBlock，得到大小同样为16*16*128的图片。对该图片做DowSample，就可以得到第三层的输入，也就是大小为8*8*128的图片

即，先同层间做channel上的变化，再不同层间做size上的变化（即图片的压缩处理），Decoder层同理

DownBlock 和 UpBlock

TimeEmbedding层采用和Transformer一致的三角函数位置编码，将常数转变为向量。Attention层则是沿着channel维度将图片拆分为token，做完attention后再重新组装成图片（注意Attention层不是必须的，是可选的，可以根据需要选择要不要上attention）

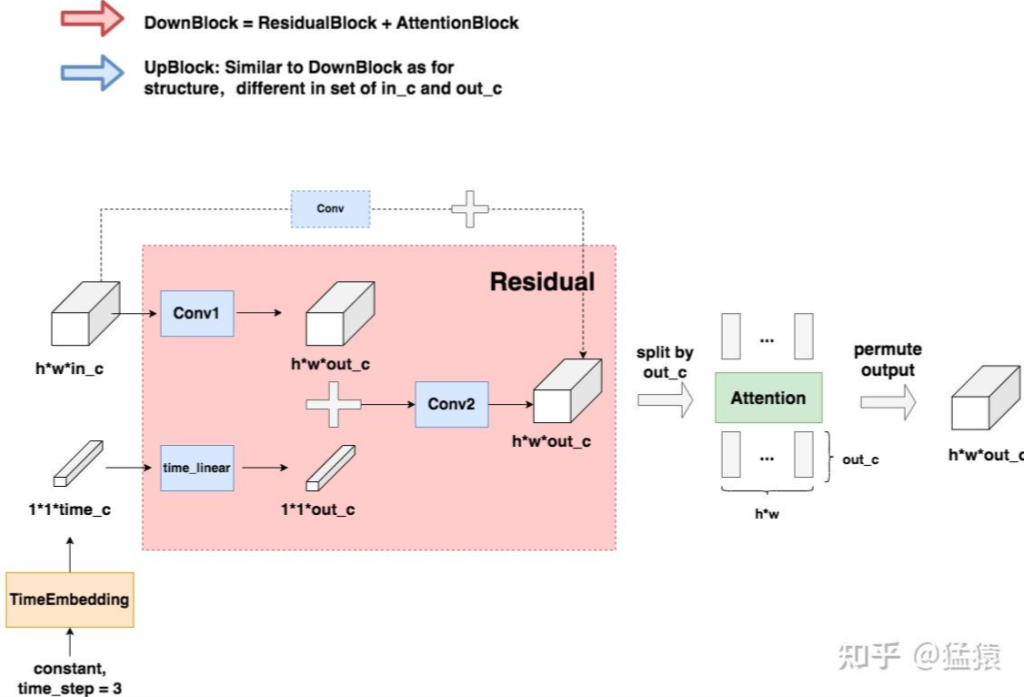
虚线部分即为“残差连接”（Residual Connection），而残差连接之上引入的虚线框Conv的意思是，如果in_c != out_c，则对in_c做一次卷积，使得其通道数等于out_c后，再相加；否则将直接相加

DownSample 和 UpSample

这个模块是压缩(Conv)和放大(ConvT)图片的过程

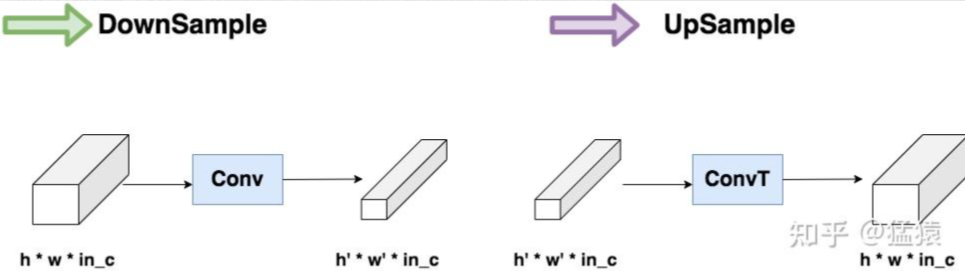
卷积和反卷积

卷积(Convolutional)：卷积在图像处理领域被广泛的应用，像滤波、边缘检测、图片锐化等，都是通过不同的卷积核来实现的。在卷积神经网络中通过卷积操作可以提取图片中的特征，低层的卷积层可以提取到图片的一些边缘、线条、角等特征，高层的卷积能够从低层的卷积层中学到更复杂的特征，从而实现到图片的分类和识别。

反卷积：反卷积也被称为转置卷积，反卷积其实就是卷积的逆过程。大家可能对于反卷积的认识有一个误区，以为通过反卷积就可以获取到经过卷积之前的图片，实际上通过反卷积操作并不能还原出卷积之前的图片，只能还原出卷积之前图片的尺寸。

那么到底反卷积有什么作用呢？通过反卷积可以用来可视化卷积的过程，反卷积在GAN等领域中有着大量的应用。

卷积

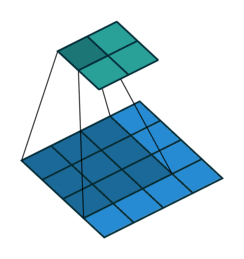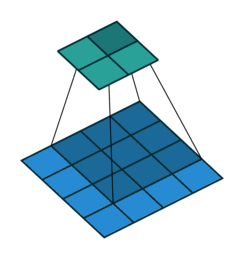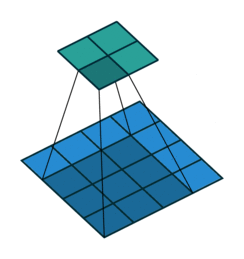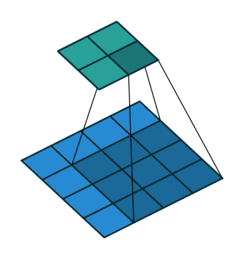
上图展示了一个卷积的过程，其中蓝色的图片(4*4)表示的是进行卷积的图片，阴影的图片(3*3)表示的是卷积核，绿色的图片(2*2)表示是进行卷积计算之后的图片。在卷积操作中有几个比较重要的参数，输入图片的尺寸、步长、卷积核的大小、输出图片的尺寸、填充大小

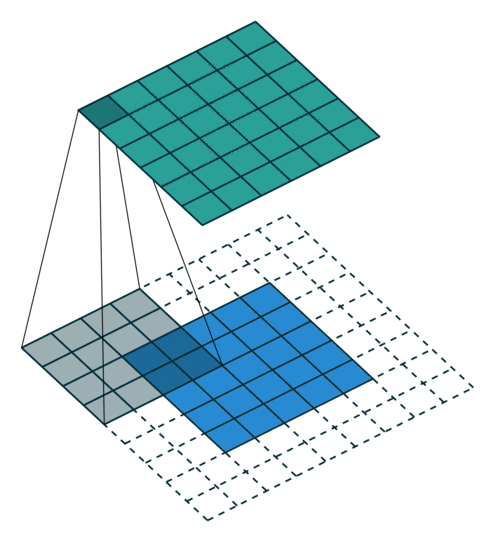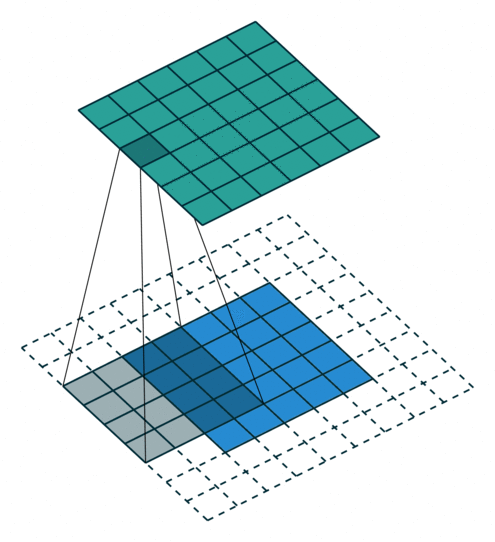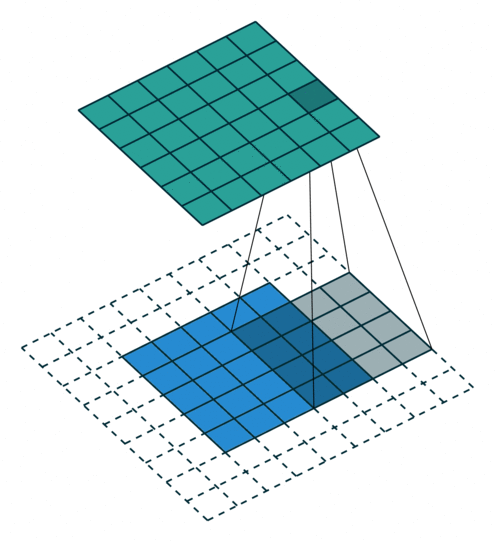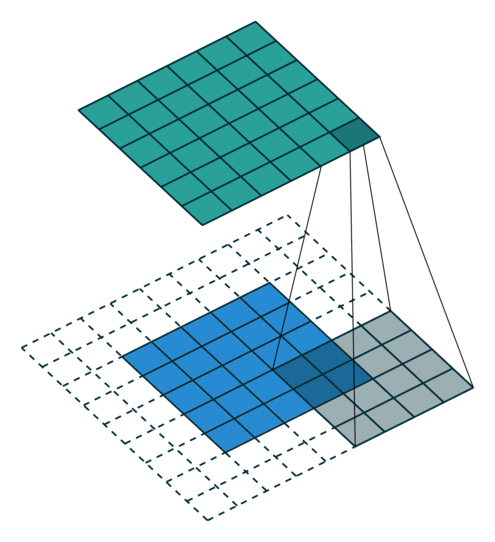
输入图片的尺寸 i：上图中的蓝色图片(5*5)，表示的是需要进行卷积操作的图片

卷积核的大小 k：上图中的会移动阴影图片表示的是卷积核(4*4)，通过不同参数不同大小的卷积核可以提取到图片的不同特征 步长 s：是指卷积核移动的长度，通过上图可以发现卷积核水平方向移动的步长和垂直方向移动的步长是一样的都是1

填充大小 p：是指在输入图片周围填充的圈数，通常都是用0来进行填充的，上图中蓝色图片周围两圈虚线的矩形表示的是填充的值，所以填充掉是2

输出图片的尺寸 o：经过卷积操作之后获取到的图片的大小，上图的绿色图片(6*6)

如果已知 i 、 k 、 p 、 s，可以求得 o，计算公式：$o=\frac{i-k+2*p}{s}+1$

反卷积

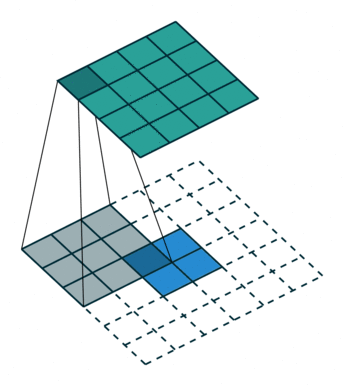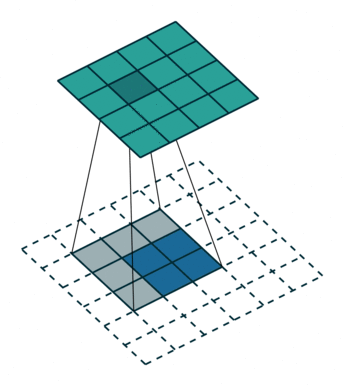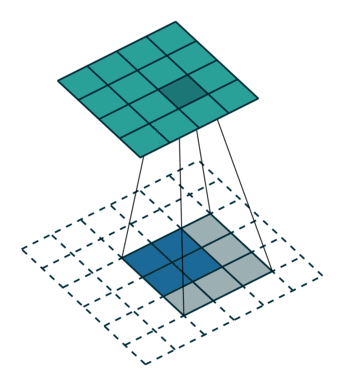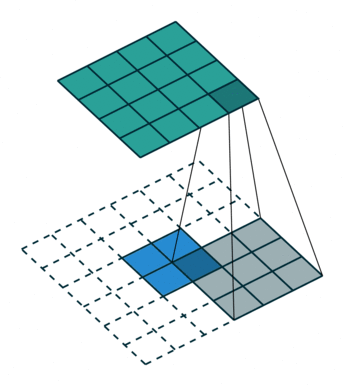
上图展示一个反卷积的工作过程，乍看一下好像反卷积和卷积的工作过程差不多，主要的区别在于反卷积输出图片的尺寸会大于输入图片的尺寸，通过增加padding来实现这一操作，上图展示的是一个strides(步长)为1的反卷积。下面看一个strides不为1的反卷积

上图中的反卷积的stride为2，通过间隔插入padding来实现的。同样，可以根据反卷积的 o 、 s 、 k 、 p参数来计算反卷积的输出 i，也就是卷积的输入。公式：$i=(o-1)*s+k-2*p$

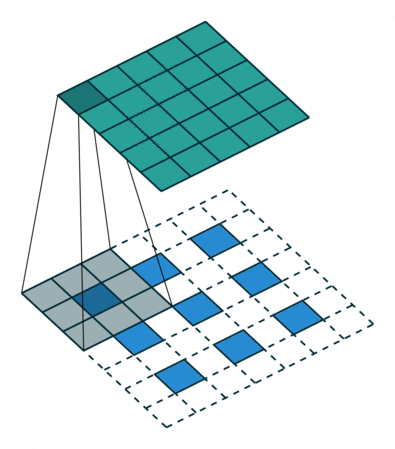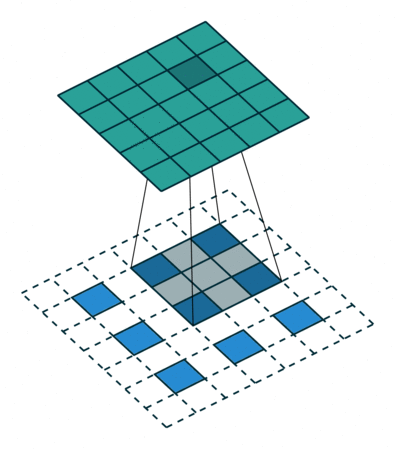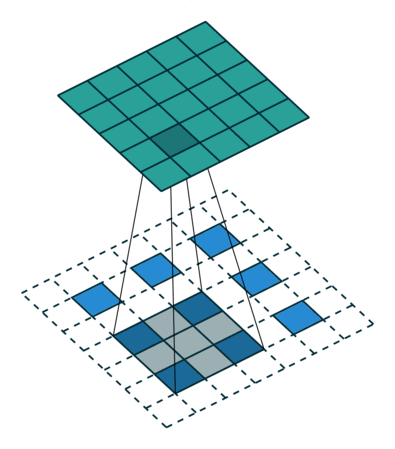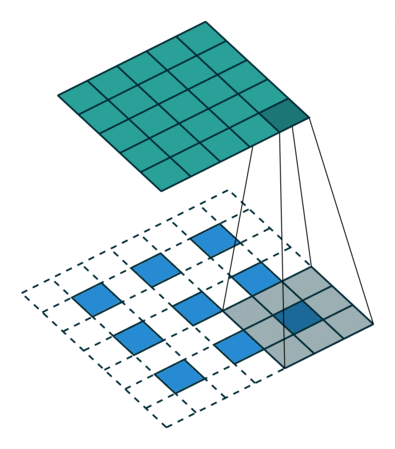
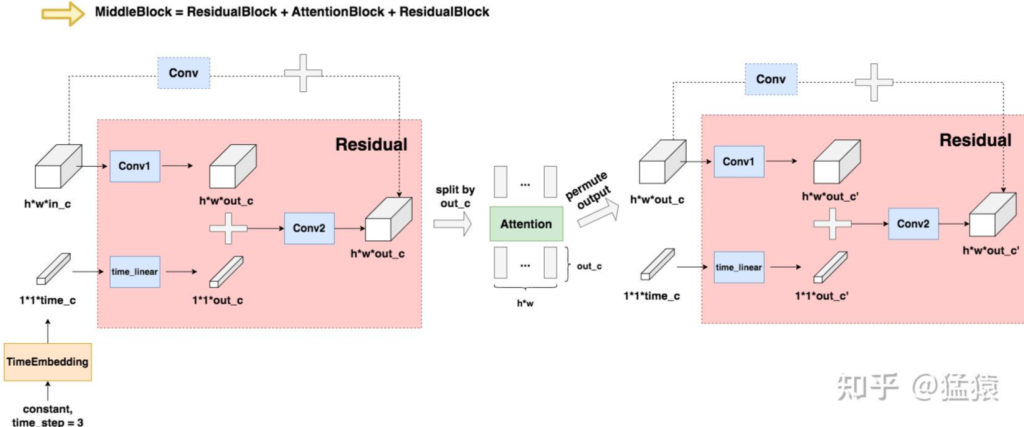
MiddleBlock

与 DownBlock 和 UpBlock 过程相似